2020江苏教师招聘面试:教案《直线的倾斜角和斜率》

　　2020江苏教师招聘面试:教案《直线的倾斜角和斜率》由江苏事业单位招聘同步江苏华图整理发布，更多江苏华图的信息内容，请关注江苏教师招聘考试频道。

　　一、教学目标

　　1.知识与技能

　　(1)正确理解直线的倾斜角和斜率的概念。

　　(2)理解直线的倾斜角的唯一性。

　　(3)理解直线的斜率的存在性。

　　(4)斜率公式的推导过程，掌握过两点的直线的斜率公式。

　　2.过程与方法目标：

　　通过师生互动，小组讨论，经历探究倾斜角和斜率，学生的观察能力，理解能力，推理能力得到提高。

　　3.情感态度与价值观:

　　(1) 通过直线的倾斜角概念的引入学习和直线倾斜角与斜率关系的揭示，培养学生观察、探索能力，运用数学语言表达能力，数学交流与评价能力.

　　(2) 通过斜率概念的建立和斜率公式的推导，帮助学生进一步理解数形结合思想，培养学生树立辩证统一的观点，培养学生形成严谨的科学态度和求简的数学精神.

　　二、重点与难点:

　　直线的倾斜角、斜率的概念和公式.

　　三、教学用具：计算机

　　四、教学方法：启发、引导、讨论.

　　五、教学过程：

　　1.直线的倾斜角的概念

　　我们知道, 经过两点有且只有(确定)一条直线. 那么, 经过一点P的直线l的位置能确定吗? 如图, 过一点P可以作无数多条直线a,b,c, …易见,答案是否定的.这些直线有什么联系呢?

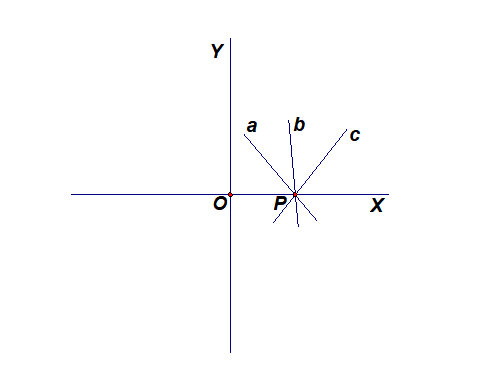
　　(1)它们都经过点P (2)它们的‘倾斜程度’不同. 怎样描述这种‘倾斜程度’的不同?

　　引入直线的倾斜角的概念:

　　当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α= 0°.

　　问: 倾斜角α的取值范围是什么? 0°≤α<180°.

　　当直线l与x轴垂直时, α= 90°.

　　因为平面直角坐标系内的每一条直线都有确定的倾斜程度, 引入直线的倾斜角之后, 我们就可以用倾斜角α来表示平面直角坐标系内的每一条直线的倾斜程度.

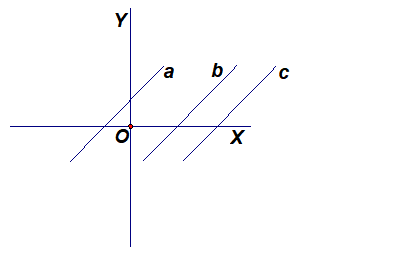
　　如图, 直线a∥b∥c, 那么它们

　　的倾斜角α相等吗? 答案是肯定的.所以一个倾斜角α不能确定一条直线.

　　确定平面直角坐标系内的一条直线位置的几何要素: 一个点P和一个倾斜角α.

　　(二)直线的斜率:

　　一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα。

　　⑴当直线l与x轴平行或重合时, α=0°, k = tan0°=0;

　　⑵当直线l与x轴垂直时, α= 90°, k 不存在.

　　由此可知, 一条直线l的倾斜角α一定存在,但是斜率k不一定存在.

　　例如, α=45°时, k = tan45°= 1;

　　α=135°时, k = tan135°= tan(180°- 45°) = - tan45°= - 1.

　　学习了斜率之后, 我们又可以用斜率来表示直线的倾斜程度.

　　(三) 直线的斜率公式:

　　给定两点P1(x1,y1),P2(x2,y2),x1≠x2,如何用两点的坐标来表示直线P1P2的斜率?

　　可用计算机作动画演示: 直线P1P2的四种情况, 并引导学生如何作辅助线。

　　斜率公式:

　　对于上面的斜率公式要注意下面四点：

　　(1) 当x1=x2时，公式右边无意义，直线的斜率不存在，倾斜角α= 90°, 直线与x轴垂直;

　　(2)k与P1、P2的顺序无关, 即y1,y2和x1,x2在公式中的前后次序可以同时交换, 但分子与分母不能交换;

　　(3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得;

　　(4) 当 y1=y2时, 斜率k = 0, 直线的倾斜角α=0°，直线与x轴平行或重合。

　　(5)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到。

　　(四)例题:

　　例1 已知A(3, 2), B(-4, 1), C(0, -1), 求直线AB, BC, CA的斜率, 并判断它们的倾斜角是钝角还是锐角.(用计算机作直线, 图略)

　　分析: 已知两点坐标, 而且x1≠x2, 由斜率公式代入即可求得k的值;

　　而当k = tanα<0时, 倾斜角α是钝角;

　　而当k = tanα>0时, 倾斜角α是锐角;

　　而当k = tanα=0时, 倾斜角α是0°。

　　略解: 直线AB的斜率k1=1/7>0, 所以它的倾斜角α是锐角;

　　直线BC的斜率k2=-0.5<0, 所以它的倾斜角α是钝角;

　　直线CA的斜率k3=1>0, 所以它的倾斜角α是锐角。

　　例2 在平面直角坐标系中, 画出经过原点且斜率分别为1, -1, 2, 及-3的直线a, b, c, l。

　　分析:要画出经过原点的直线a, 只要再找出a上的另外一点M. 而M的坐标可以根据直线a的斜率确定; 或者k=tanα=1是特殊值,所以也可以以原点为角的顶点,x 轴的正半轴为角的一边, 在x 轴的上方作45°的角, 再把所作的这一边反向延长成直线即可.

　　略解: 设直线a上的另外一点M的坐标为(x,y),根据斜率公式有

　　1=(y-0)/(x-0)

　　所以 x = y

　　可令x = 1, 则y = 1, 于是点M的坐标为(1,1).此时过原点和点

　　M(1,1), 可作直线a.

　　同理, 可作直线b, c, l.(用计算机作动画演示画直线过程)

　　(五)练习: P91 1. 2. 3. 4.

　　(六)小结: (1)直线的倾斜角和斜率的概念。 (2) 直线的斜率公式。

　　w.w.w.k.s.5.u.c.o.m

　　w.w.w.k.s.5.u.c.o.m

　　以上即为《2020江苏教师招聘面试:教案《直线的倾斜角和斜率》》全文，[点击查看]更多江苏教师招考公告，关注江苏教师招聘考试，了解更多考试资讯。

（编辑：admin）